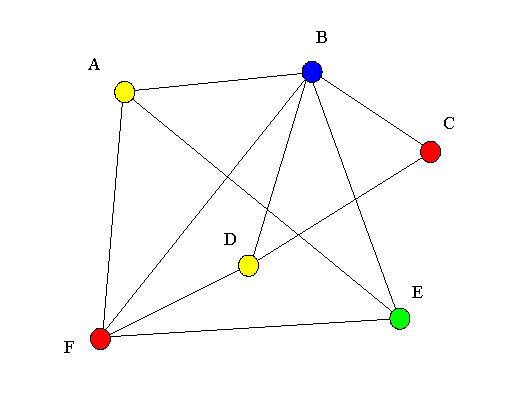
Déterminer le nombre chromatique du graphe suivant :
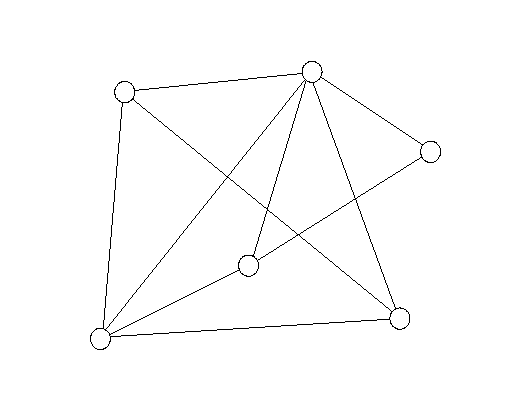
Analyse
On procède classiquement en majorant le nombre chromatique. Une minoration intéressante est ici possible (regardez bien !). Le coloriage du graphe permet de conclure.
Résolution
Nous appelons G le graphe proposé.
Commençons par nommer les sommets du graphe :
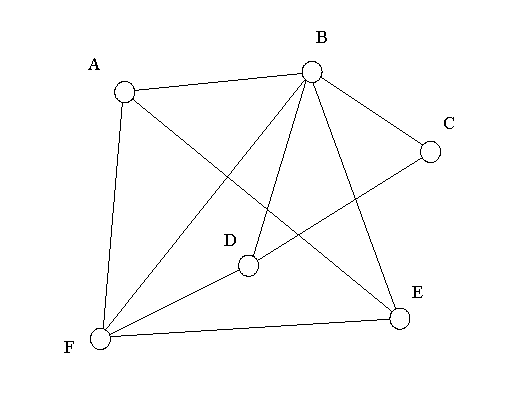
On a facilement les degrés des sommets :
|
Sommet |
A |
B |
C |
D |
E |
F |
|
Degré |
3 |
5 |
2 |
3 |
3 |
4 |
Le sommet B est le sommet de plus haut degré.
On a alors immédiatement la majoration suivante du nombre chromatique :
On constate que le sous-graphe ABEF est complet. Son nombre chromatique vaut donc 4 et minore celui de G :
Utilisons alors l’algorithme du cours pour colorer G.
On classe d’abord les sommets pas degré décroissant :
|
Sommet |
B |
F |
A |
D |
E |
C |
|
Degré |
5 |
4 |
3 |
3 |
3 |
2 |
On procède ensuite au coloriage :
|
Sommet |
B |
F |
A |
D |
E |
C |
|
Degré |
5 |
4 |
3 |
3 |
3 |
2 |
|
Couleur |
|
|
|
|
|
|
Nous avons pu colorer le graphe à l’aide de 4 couleurs. Du fait de la minoration ci-dessus, il n’est pas possible d’en utiliser moins.
Résultat final